## 人世间最痛苦的事情，就是，年轻时能做到的事情，老了就做不到了。
##你们谁能摸到，踩着我的肩膀，去摸一下那个，游戏之神特图的，星杯。
---
## 比方说算法就在眼前，就是看不懂。
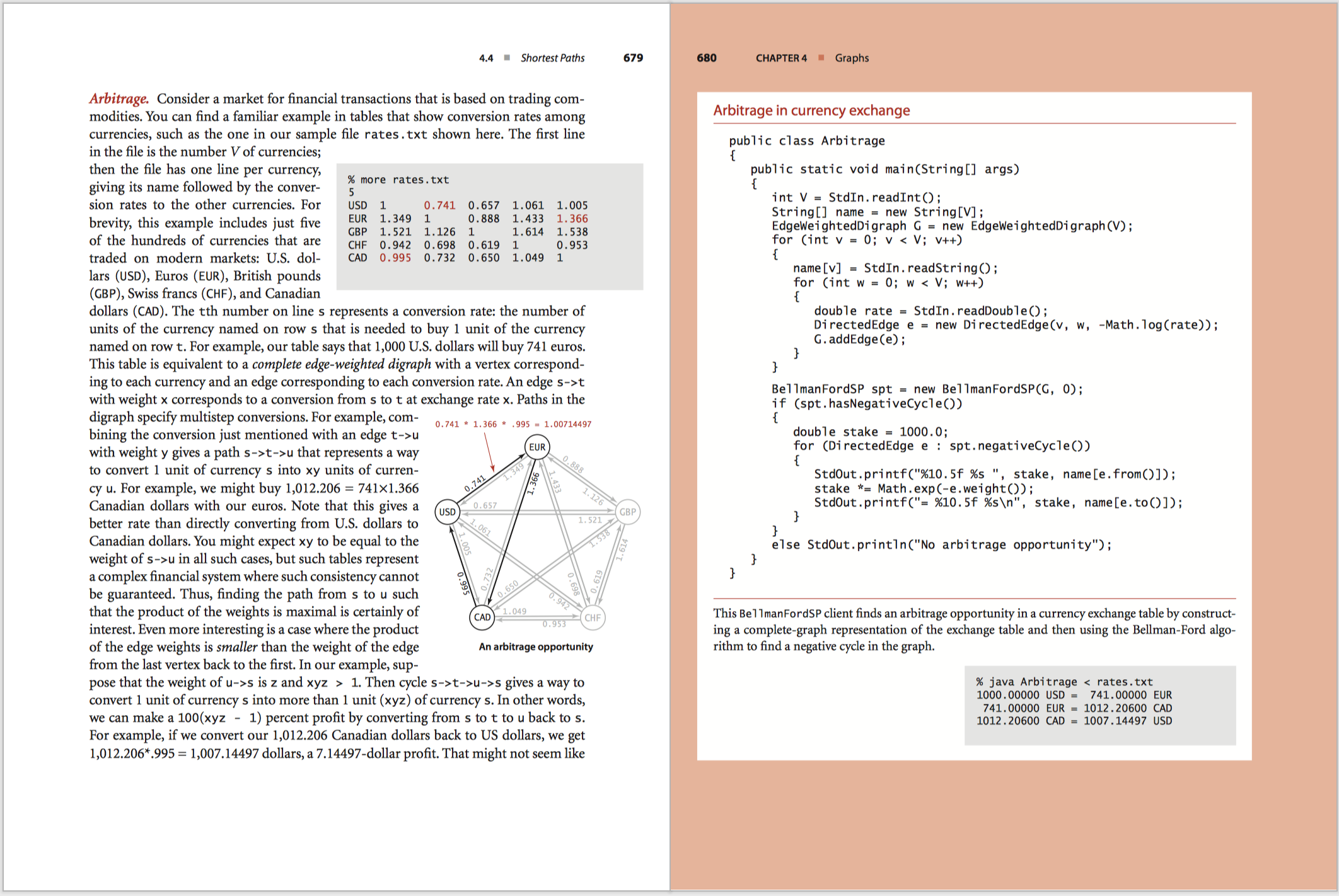
```
public class Arbitrage
{
public static void main(String[] args)
{
int V = StdIn.readInt();
String[] name = new String[V];
EdgeWeightedDigraph G = new EdgeWeightedDigraph(V);
for (int v = 0; v < V; v++)
{
name[v] = StdIn.readString();
for (int w = 0; w < V; w++)
{
double rate = StdIn.readDouble();
DirectedEdge e = new DirectedEdge(v, w, -Math.log(rate));
G.addEdge(e);
}
}
BellmanFordSP spt = new BellmanFordSP(G, 0);
if (spt.hasNegativeCycle())
{
double stake = 1000.0;
for (DirectedEdge e : spt.negativeCycle())
{
StdOut.printf(".5f %s ", stake, name[e.from()]);
stake *= Math.exp(-e.weight());
StdOut.printf("= .5f %s\n", stake, name[e.to()]);
}
}
else StdOut.println("No arbitrage opportunity");
}
}
```
---
## 比方说代码就在眼前，就是实现不了。
https://www.dailycodingproblem.com/blog/how-to-find-arbitrage-opportunities-in-python/
```
from math import log
def arbitrage(table):
transformed_graph = [[-log(edge) for edge in row] for row in graph]
# Pick any source vertex -- we can run Bellman-Ford from any vertex and
# get the right result
source = 0
n = len(transformed_graph)
min_dist = [float('inf')] * n
min_dist[source] = 0
# Relax edges |V - 1| times
for i in range(n - 1):
for v in range(n):
for w in range(n):
if min_dist[w] > min_dist[v] + transformed_graph[v][w]:
min_dist[w] = min_dist[v] + transformed_graph[v][w]
# If we can still relax edges, then we have a negative cycle
for v in range(n):
for w in range(n):
if min_dist[w] > min_dist[v] + transformed_graph[v][w]:
return True
return False
```
---
## 比方说架构图就在眼前，就是搭不出来。
---
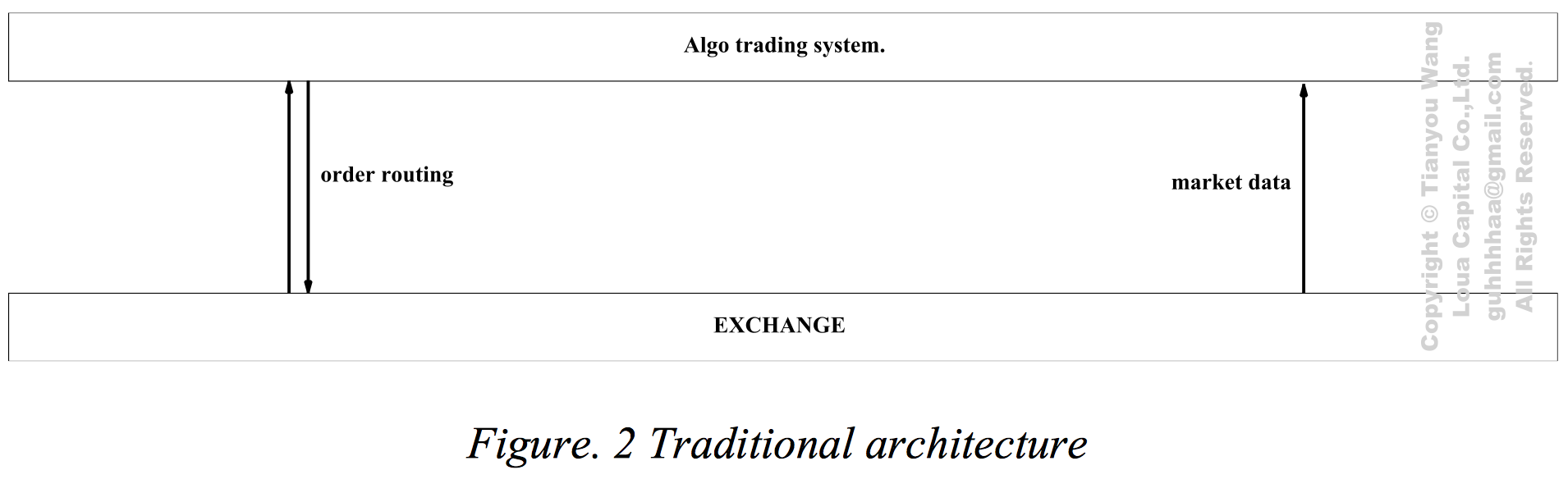
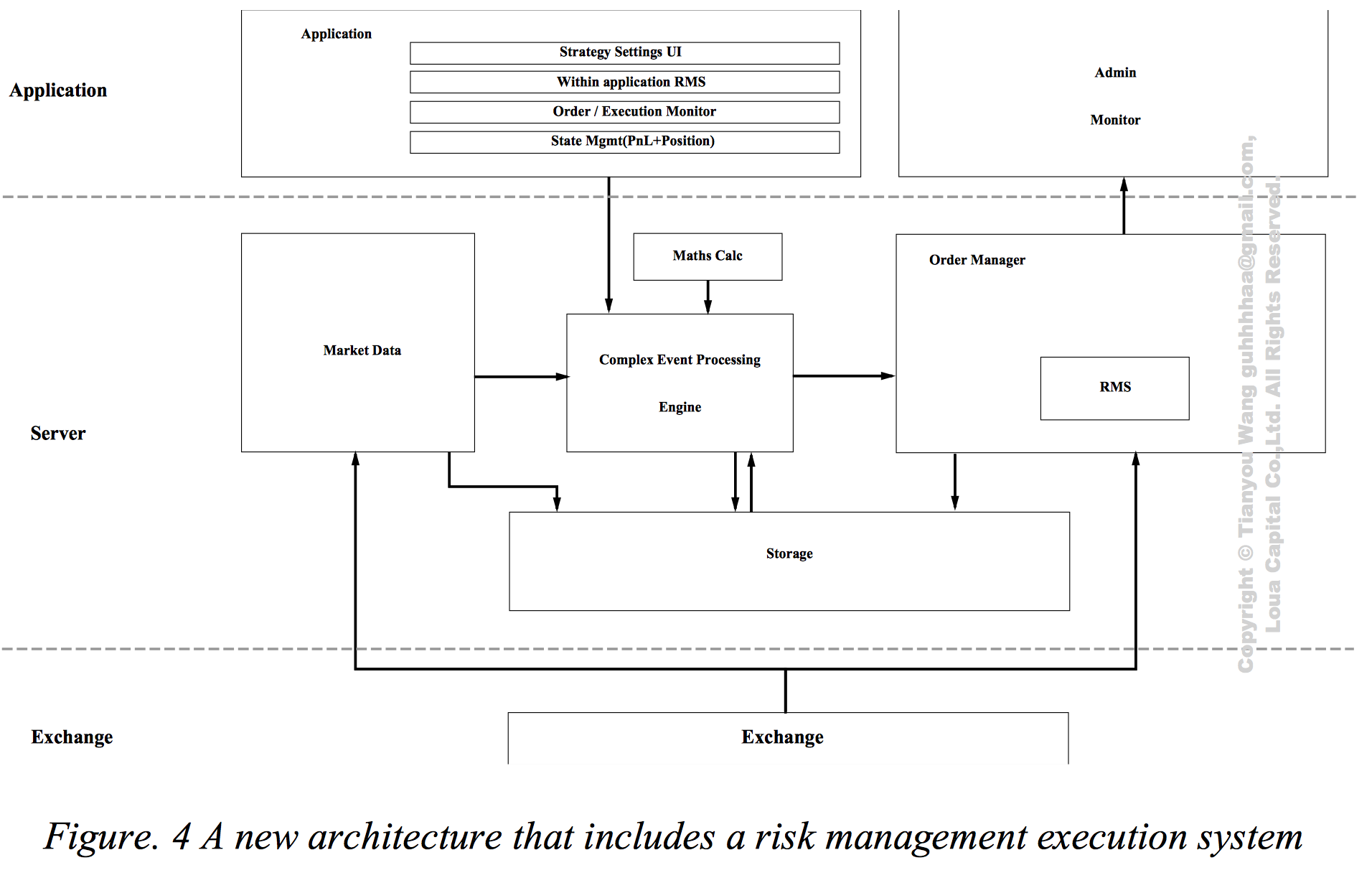
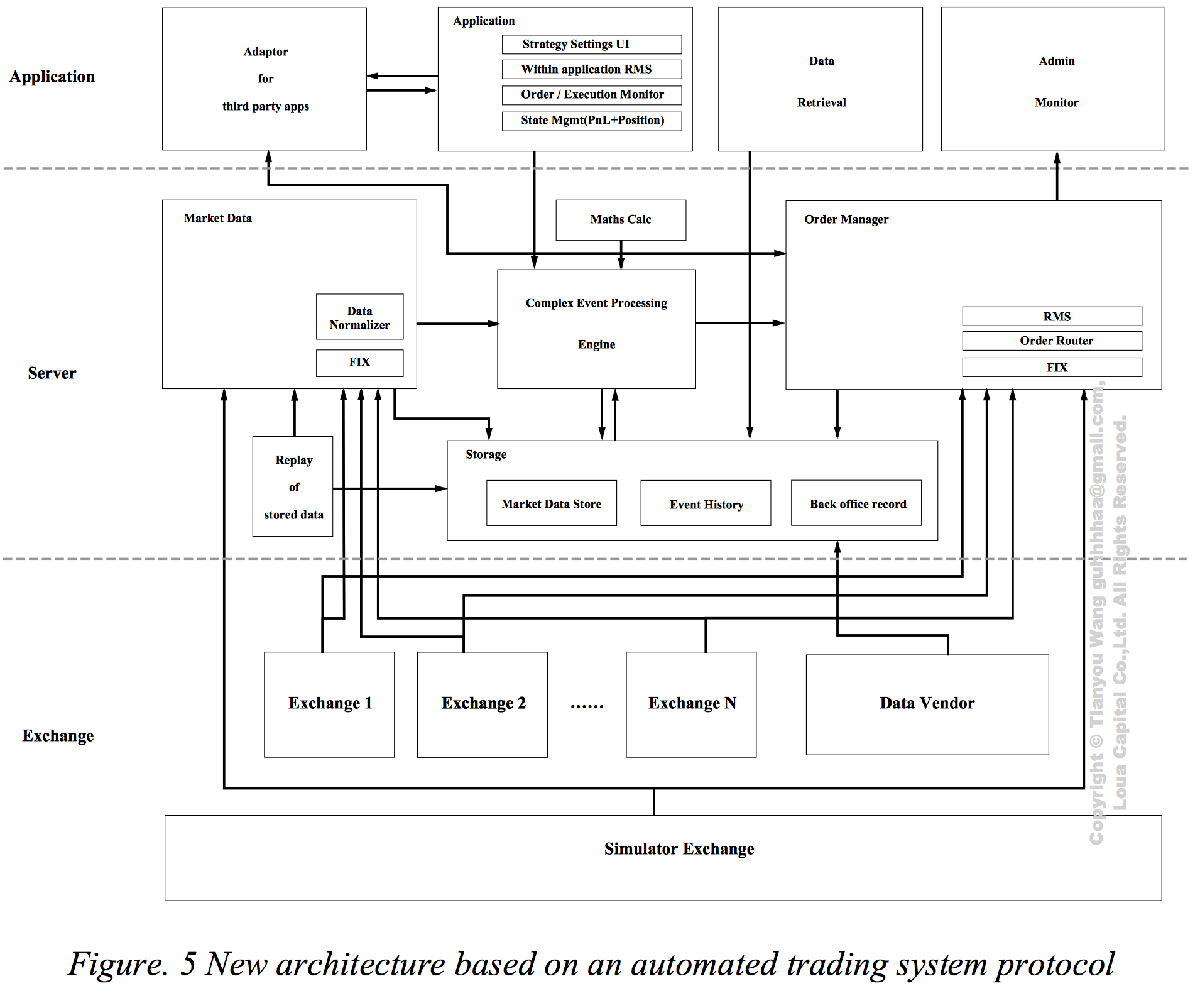
## 仅以此贴，记录我对星杯的探索过程，只能等日后，其他人来复现它了。
## 市场是有圣杯的，就是Bellman-Ford-Moore算法，用于外汇现货多角套利。
雪球
